5y 1 6x 4y 10
paulzimmclay
Sep 23, 2025 · 6 min read
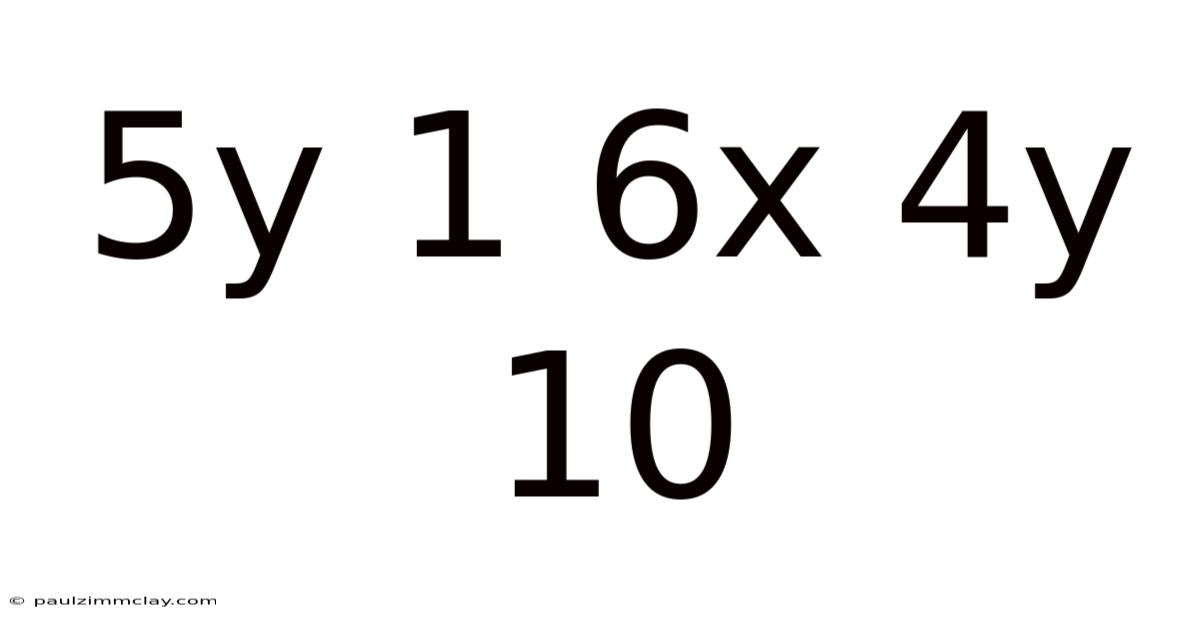
Table of Contents
Deciphering 5y + 1 = 6x + 4y + 10: A Comprehensive Exploration of Linear Equations
This article delves into the solution and implications of the linear equation 5y + 1 = 6x + 4y + 10. We'll explore various approaches to solving this equation, discuss its graphical representation, and examine its application in different mathematical contexts. Understanding this seemingly simple equation opens doors to a broader comprehension of linear algebra and its real-world applications. This exploration will be suitable for students and anyone interested in enhancing their mathematical skills.
Introduction: Understanding the Equation
The equation 5y + 1 = 6x + 4y + 10 represents a linear equation in two variables, x and y. Linear equations are characterized by their straight-line graphical representation. Solving this equation means finding the values of x and y that make the equation true. Because we have two variables and only one equation, we won't arrive at a single, unique solution. Instead, we'll find a relationship between x and y, which can be represented as a line on a graph.
Step-by-Step Solution: Simplifying and Rearranging
Our first step is to simplify the equation by combining like terms. We can start by subtracting 4y from both sides:
5y + 1 - 4y = 6x + 4y + 10 - 4y
This simplifies to:
y + 1 = 6x + 10
Next, we subtract 1 from both sides:
y + 1 - 1 = 6x + 10 - 1
This gives us:
y = 6x + 9
This is the simplified form of our equation. It's now in the slope-intercept form (y = mx + b), where 'm' represents the slope (6 in this case) and 'b' represents the y-intercept (9).
Graphical Representation: Visualizing the Solution
The equation y = 6x + 9 can be easily graphed. The y-intercept is 9, meaning the line crosses the y-axis at the point (0, 9). The slope is 6, which means for every 1 unit increase in x, y increases by 6 units.
To graph this, start at the point (0, 9). Then, move one unit to the right (increase x by 1) and six units up (increase y by 6). This gives you another point on the line, (1, 15). You can continue this process to plot several points and draw a straight line through them. This line represents all the possible (x, y) pairs that satisfy the original equation 5y + 1 = 6x + 4y + 10.
Mathematical Implications: Slope, Intercept, and Solutions
The slope of the line (6) indicates the rate of change of y with respect to x. For every unit increase in x, y increases by 6 units. This constant rate of change is a key characteristic of linear relationships.
The y-intercept (9) represents the value of y when x is 0. It's the point where the line intersects the y-axis.
Since we have an infinite number of points on the line, there are infinitely many solutions to the equation 5y + 1 = 6x + 4y + 10. Each point (x, y) on the line represents a solution that satisfies the equation.
Solving for Specific Values:
While there are infinitely many solutions, we can find specific solutions by substituting a value for either x or y and solving for the other variable. For example:
- If x = 0: y = 6(0) + 9 = 9. Therefore, (0, 9) is a solution.
- If y = 0: 0 = 6x + 9. Solving for x, we get x = -1.5. Therefore, (-1.5, 0) is a solution.
- If x = 2: y = 6(2) + 9 = 21. Therefore, (2, 21) is a solution.
Extending the Understanding: Systems of Equations
To find a unique solution to a system involving x and y, we would need a second independent linear equation involving x and y. This second equation would represent a different line. The solution to the system of equations would be the point where the two lines intersect. This intersection point represents the unique (x, y) pair that satisfies both equations simultaneously.
For example, if we had the system:
- 5y + 1 = 6x + 4y + 10
- y = 2x + 1
We could substitute the second equation into the simplified form of the first equation (y = 6x + 9):
2x + 1 = 6x + 9
Solving this equation for x, we would find a single value for x, which can then be substituted back into either equation to find the corresponding value for y. This would give us a unique solution (x, y) that satisfies both equations.
Real-World Applications: Linear Relationships in Various Fields
Linear equations are fundamental to many areas of science, engineering, and economics. They model situations where there's a constant rate of change between two variables. Examples include:
- Physics: Calculating velocity and displacement using constant acceleration.
- Engineering: Modeling relationships between stress and strain in materials.
- Economics: Analyzing supply and demand curves, predicting costs based on production levels.
- Finance: Calculating simple interest.
The equation 5y + 1 = 6x + 4y + 10, while seemingly simple, provides a foundation for understanding these broader applications. The ability to manipulate and solve such equations is crucial for tackling more complex mathematical problems in these fields.
Frequently Asked Questions (FAQ)
-
Q: What if I get a different simplified equation? A: As long as you follow the rules of algebra (adding, subtracting, multiplying, and dividing both sides of the equation by the same non-zero value), you should arrive at an equivalent equation. Different forms of the equation (e.g., 6x - y = -9) still represent the same line.
-
Q: Why are there infinitely many solutions? A: Because we have only one equation with two unknowns (x and y). This means there are many combinations of x and y that can satisfy the equation. To obtain a unique solution, you need as many independent equations as you have unknowns.
-
Q: How do I check if my solution is correct? A: Substitute the x and y values of your solution back into the original equation (5y + 1 = 6x + 4y + 10). If both sides of the equation are equal, then your solution is correct.
-
Q: What is the significance of the slope and y-intercept? A: The slope indicates the rate of change between x and y. The y-intercept is the point where the line intersects the y-axis, representing the value of y when x is zero.
Conclusion: A Foundation for Further Exploration
This comprehensive exploration of the linear equation 5y + 1 = 6x + 4y + 10 demonstrates the fundamental concepts of solving and interpreting linear equations. Understanding this seemingly simple equation lays a strong foundation for tackling more complex mathematical problems. The principles covered—simplification, graphical representation, slope, y-intercept, and the concept of systems of equations—are crucial for success in higher-level mathematics and its applications across diverse fields. Remember, the journey of mastering mathematics is built step-by-step, and understanding linear equations is a significant milestone in that journey. Continue practicing and exploring, and you'll find your mathematical abilities growing exponentially.
Latest Posts
Latest Posts
-
Which Statement Describes Dramatic Irony
Sep 24, 2025
-
Sensation Is To Perception As
Sep 24, 2025
-
Krebs Cycle Inputs And Outputs
Sep 24, 2025
-
Hair Follicle Under Microscope Labeled
Sep 24, 2025
-
Food Chain Gizmo Answer Key
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 5y 1 6x 4y 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.