Factor X 2 8x 15
paulzimmclay
Sep 16, 2025 · 6 min read
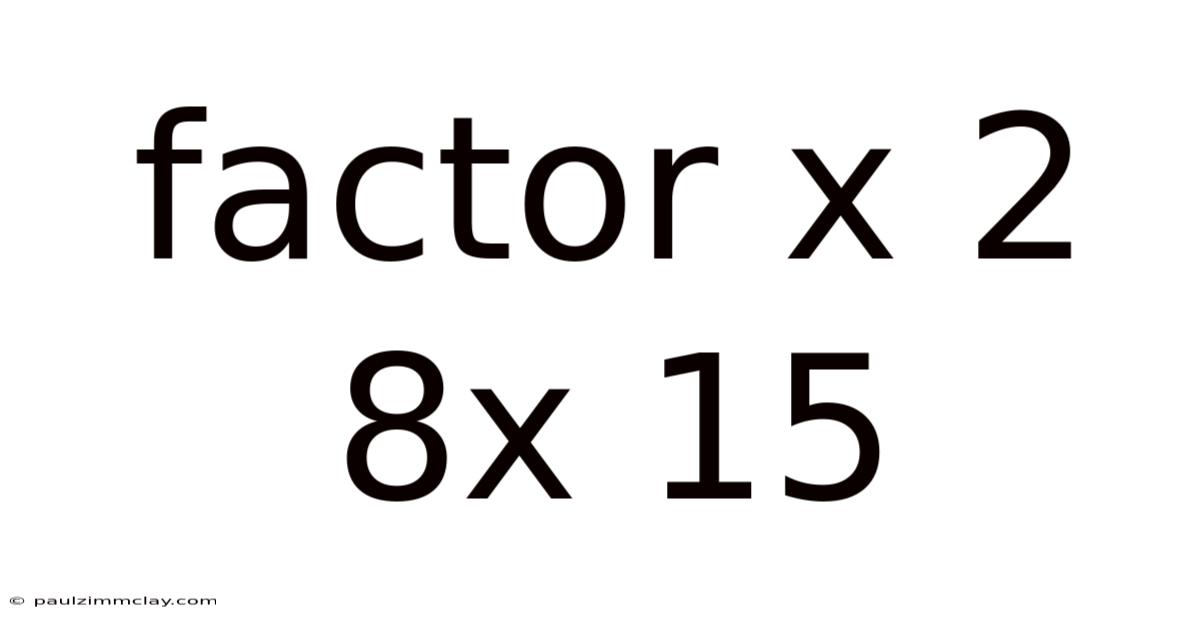
Table of Contents
Factoring the Quadratic Expression: x² + 8x + 15
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This article will guide you through the process of factoring the specific quadratic expression x² + 8x + 15, providing a step-by-step explanation, exploring different methods, and delving into the underlying mathematical principles. We'll also address frequently asked questions to ensure a comprehensive understanding of this topic. This will empower you to tackle similar problems with confidence.
Introduction: What is Factoring?
Factoring, in the context of algebra, is the process of finding what to multiply together to get an expression. It's like reverse multiplication. We start with a polynomial (in this case, a quadratic expression because it's a polynomial of degree 2) and break it down into simpler expressions that, when multiplied, give us the original expression. Factoring is a crucial skill for solving quadratic equations, simplifying expressions, and understanding many other algebraic concepts.
Our target expression is x² + 8x + 15. This is a trinomial because it has three terms. Our goal is to rewrite it as a product of two binomials, expressions with two terms.
Method 1: The "AC" Method (for Trinomials of the form ax² + bx + c)
This method is particularly helpful for factoring trinomials where the coefficient of x² (which is 'a' in the general form ax² + bx + c) is not 1. While our example has a=1, understanding this method provides a more robust approach for handling more complex quadratic expressions.
-
Identify a, b, and c: In our expression, x² + 8x + 15, a = 1, b = 8, and c = 15.
-
Find two numbers that multiply to ac and add up to b: We need two numbers that multiply to (a)(c) = (1)(15) = 15 and add up to b = 8. These numbers are 3 and 5 (because 3 x 5 = 15 and 3 + 5 = 8).
-
Rewrite the middle term: Rewrite the middle term (8x) using the two numbers we found: x² + 3x + 5x + 15.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair: x(x + 3) + 5(x + 3)
-
Factor out the common binomial: Notice that (x + 3) is a common factor in both terms. Factor it out: (x + 3)(x + 5)
Therefore, the factored form of x² + 8x + 15 is (x + 3)(x + 5).
Method 2: Trial and Error (for Trinomials with a = 1)
This method is quicker for trinomials where the coefficient of x² is 1.
-
Set up the binomial factors: Since a = 1, we can start by setting up two binomials like this: (x )(x ).
-
Find factors of c that add up to b: We need two numbers that multiply to 15 (our c value) and add up to 8 (our b value). These numbers, as we found before, are 3 and 5.
-
Fill in the binomials: Place the numbers 3 and 5 into the binomials: (x + 3)(x + 5).
This directly gives us the factored form: (x + 3)(x + 5).
Expanding the Factored Form (Verification)
To verify that our factoring is correct, we can expand the factored form using the FOIL method (First, Outer, Inner, Last):
(x + 3)(x + 5) = x² + 5x + 3x + 15 = x² + 8x + 15
This matches our original expression, confirming that our factoring is accurate.
Solving Quadratic Equations using Factoring
Factoring is a key technique for solving quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0. If we can factor the quadratic expression, we can use the zero-product property to find the solutions (roots) of the equation.
The zero-product property states that if the product of two factors is zero, then at least one of the factors must be zero.
For example, if we want to solve the equation x² + 8x + 15 = 0, we can use our factored form:
(x + 3)(x + 5) = 0
This means either (x + 3) = 0 or (x + 5) = 0. Solving these gives us the solutions x = -3 and x = -5. These are the roots or zeros of the quadratic equation.
Understanding the Relationship Between Roots and Factors
There's a direct relationship between the roots of a quadratic equation and the factors of the corresponding quadratic expression. If r1 and r2 are the roots of the equation ax² + bx + c = 0, then the factored form of the quadratic expression is a(x - r1)(x - r2).
In our case, the roots are -3 and -5. Therefore, the factored form is 1(x - (-3))(x - (-5)) = (x + 3)(x + 5), which confirms our previous results.
The Significance of Factoring in Higher-Level Mathematics
Factoring quadratic expressions is not just a skill for basic algebra. It forms the foundation for more advanced concepts in mathematics, including:
- Solving polynomial equations of higher degrees: The principles of factoring extend to polynomials with degrees greater than 2.
- Partial fraction decomposition: This technique, used in calculus and other advanced areas, relies heavily on factoring.
- Rational functions: Understanding factoring is crucial for analyzing and simplifying rational functions.
- Calculus: Factoring simplifies expressions encountered in differentiation and integration.
Frequently Asked Questions (FAQ)
Q1: What if the quadratic expression cannot be factored?
A1: Not all quadratic expressions can be factored using integers. In such cases, you can use the quadratic formula to find the roots, or you can approximate the roots using numerical methods.
Q2: Is there only one way to factor a quadratic expression?
A2: No, sometimes there might be multiple equivalent ways to factor a quadratic expression, but the resulting factors will always multiply back to the original expression. For example, you could express 2(x+3)(x+5) and it would be equally valid. However, generally, we aim for the simplest and fully factored form.
Q3: How can I improve my factoring skills?
A3: Practice is key! Work through many different examples, starting with simpler expressions and gradually increasing the complexity. Focus on understanding the underlying principles, not just memorizing steps. Use online resources, textbooks, and practice problems to reinforce your learning.
Q4: What are some common mistakes to avoid when factoring?
A4: Common mistakes include incorrect signs, forgetting to check your work by expanding the factored form, and not considering all possible factor pairs. Always double-check your work and be meticulous in your calculations.
Conclusion: Mastering the Art of Factoring
Factoring quadratic expressions, such as x² + 8x + 15, is a fundamental algebraic skill with far-reaching applications. By understanding the different methods, such as the AC method and the trial-and-error approach, and practicing regularly, you can confidently tackle more complex algebraic problems. Remember the importance of verifying your work and appreciating the connection between factoring, roots, and the broader landscape of mathematics. Mastering factoring will not only improve your algebraic abilities but will also pave the way for success in more advanced mathematical studies. The seemingly simple task of factoring lays the foundation for much more complex mathematical concepts.
Latest Posts
Latest Posts
-
Latent Learning Ap Psychology Definition
Sep 16, 2025
-
Twitch From The Movie Holes
Sep 16, 2025
-
Exclusive Right To Sell Listing
Sep 16, 2025
-
To Cause Cancer Proto Oncogenes Require
Sep 16, 2025
-
Military Sorority Kappa Epsilon Psi
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 8x 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.