The Diagram Represents 6x2-7x 2
paulzimmclay
Sep 16, 2025 · 6 min read
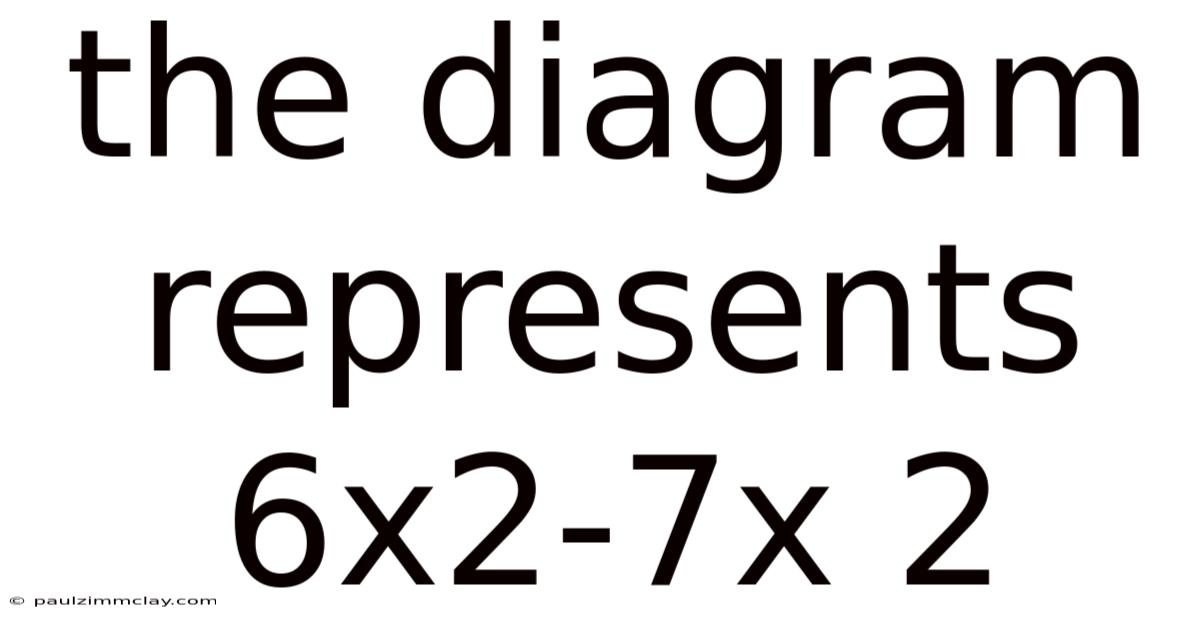
Table of Contents
Decoding the Diagram: A Deep Dive into 6x² - 7x²
This article explores the mathematical expression 6x² - 7x², breaking down its components, demonstrating its simplification, and exploring its graphical representation. We'll delve into the concepts of algebraic manipulation, quadratic expressions, and the visual interpretation of mathematical functions. Understanding this seemingly simple expression provides a strong foundation for more complex algebraic and graphical concepts. This guide is designed for students and anyone looking to strengthen their understanding of fundamental algebra.
Understanding the Components: Variables, Coefficients, and Exponents
Before tackling the expression itself, let's define its key components:
-
Variable (x): In mathematics, a variable represents an unknown quantity or a quantity that can change. In our expression, 'x' is the variable. It's a placeholder for a numerical value.
-
Coefficient: A coefficient is the numerical factor that multiplies a variable. In 6x², 6 is the coefficient of x². Similarly, in -7x², -7 is the coefficient. The coefficient indicates the scale or magnitude of the variable's contribution.
-
Exponent (²): The exponent, or power, indicates how many times the variable is multiplied by itself. In both terms, 6x² and -7x², the exponent is 2, meaning x is multiplied by itself (x * x). This signifies a quadratic expression.
Simplifying the Expression: Combining Like Terms
The expression 6x² - 7x² contains like terms. Like terms have the same variable raised to the same power. This allows us to simplify the expression using basic algebraic rules. The process is straightforward:
-
Identify like terms: Both 6x² and -7x² are like terms because they both contain x² .
-
Combine the coefficients: Add or subtract the coefficients of the like terms. In this case, we have 6 - 7 = -1.
-
Write the simplified expression: The simplified expression is -1x², which is usually written as -x².
Therefore, 6x² - 7x² = -x²
This simplification demonstrates the fundamental concept of combining like terms—a crucial skill in algebra. This principle applies to more complex expressions involving multiple variables and exponents.
Graphical Representation: Visualizing the Quadratic Function
The simplified expression, -x², represents a quadratic function. Quadratic functions are characterized by the presence of a variable raised to the power of 2. Their graphs are parabolas—U-shaped curves.
To visualize -x², consider plotting points on a coordinate plane (x-y plane). Assign various values to 'x' and calculate the corresponding values of -x². For example:
| x | -x² | (x, -x²) |
|---|---|---|
| -2 | -4 | (-2, -4) |
| -1 | -1 | (-1, -1) |
| 0 | 0 | (0, 0) |
| 1 | -1 | (1, -1) |
| 2 | -4 | (2, -4) |
Plotting these points and connecting them smoothly reveals an inverted parabola. The parabola opens downwards because the coefficient of x² is negative (-1). The vertex of the parabola, the highest point, is at the origin (0,0).
The graph visually represents the relationship between the input values (x) and the output values (-x²). For any given 'x', the corresponding '-x²' value is easily read from the graph. This graphical representation provides an intuitive understanding of how the quadratic function behaves.
Extending the Concept: More Complex Quadratic Expressions
The principles discussed above can be extended to more complex quadratic expressions. For example, consider the expression 3x² + 5x - 2. This expression contains three terms:
- 3x² (quadratic term)
- 5x (linear term)
- -2 (constant term)
While we can't directly combine these terms like we did with 6x² - 7x², we can still analyze and manipulate this expression. The graphical representation of 3x² + 5x - 2 will also be a parabola, but its vertex and orientation will differ from -x² due to the presence of the linear and constant terms. These additional terms shift and scale the parabola.
Solving for the roots (x-intercepts) of 3x² + 5x - 2 would involve techniques like factoring, the quadratic formula, or completing the square. These methods find the values of 'x' where the parabola intersects the x-axis (where y = 0).
Real-World Applications: Where Quadratic Functions Appear
Quadratic functions are not merely abstract mathematical concepts; they have significant real-world applications. They appear in various fields, including:
-
Physics: Describing projectile motion (the path of a ball thrown in the air). Gravity's influence creates a parabolic trajectory.
-
Engineering: Designing bridges, arches, and parabolic reflectors (used in satellite dishes and telescopes). The parabolic shape is crucial for focusing energy or signals.
-
Economics: Modeling supply and demand curves, where quadratic equations can represent relationships between price and quantity.
-
Computer Graphics: Creating curved lines and surfaces in computer-generated imagery (CGI) and video games.
Understanding quadratic functions like -x² provides a foundation for comprehending and modeling these real-world phenomena.
Frequently Asked Questions (FAQ)
Q: What if the expression had more than one variable?
A: If the expression involved multiple variables (e.g., 6x²y - 7x²y), you would follow the same principle of combining like terms. The like terms would have the same variables raised to the same powers. For instance, 6x²y - 7x²y simplifies to -x²y.
Q: Can I always simplify expressions by combining like terms?
A: Yes, you can always combine like terms. However, if an expression contains unlike terms (terms with different variables or different powers of the same variable), you cannot simplify further by combining them. For example, 3x² + 5x cannot be simplified further.
Q: How do I graph more complicated quadratic expressions?
A: Graphing more complex quadratic expressions often involves using graphing calculators or software. You can also use techniques such as finding the vertex, x-intercepts, and y-intercept to sketch the graph manually.
Q: What does the sign of the coefficient of x² tell us about the parabola?
A: The sign of the coefficient of x² determines the orientation of the parabola. A positive coefficient indicates a parabola that opens upwards (U-shaped), while a negative coefficient indicates a parabola that opens downwards (inverted U-shaped).
Q: What is the difference between a quadratic expression and a quadratic equation?
A: A quadratic expression is a mathematical phrase containing a variable raised to the power of 2 (and possibly other terms). A quadratic equation is a statement that sets a quadratic expression equal to zero (e.g., 3x² + 5x - 2 = 0). Solving a quadratic equation means finding the values of x that satisfy the equation.
Conclusion: Mastering the Fundamentals
The seemingly simple expression 6x² - 7x² provides a gateway to understanding fundamental algebraic concepts and their visual representations. The ability to simplify expressions, identify like terms, and interpret graphical representations of quadratic functions is essential for progressing in mathematics and numerous related fields. The process of simplification and graphical analysis underscores the power of algebraic manipulation and the interplay between symbolic and visual representations in mathematics. By mastering these basic principles, you build a solid foundation for tackling more complex mathematical problems and real-world applications. Remember, the key is to break down complex problems into smaller, manageable steps, just as we did with this simple yet insightful quadratic expression.
Latest Posts
Latest Posts
-
Adp 7 0 Board Questions
Sep 17, 2025
-
The Respiratory Membrane Consists Of
Sep 17, 2025
-
Principles Of Real Estate 1
Sep 17, 2025
-
A Coworker Didnt Clean Walmart
Sep 17, 2025
-
Cuban Missile Crisis Apush Definition
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about The Diagram Represents 6x2-7x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.